董小龙

小明：老师，我们为什么要进行碎屑统计？

沉积学家：碎屑统计是沉积物源分析中广泛而普遍使用的一种定量方法，是确定砂及砂岩的物质组成、判定其物源的重要手段。通常选取具有代表性的砂或砂岩样品磨制成薄片，在显微镜下进行定量统计。统计方法大致可分为点记法和面积法两类。

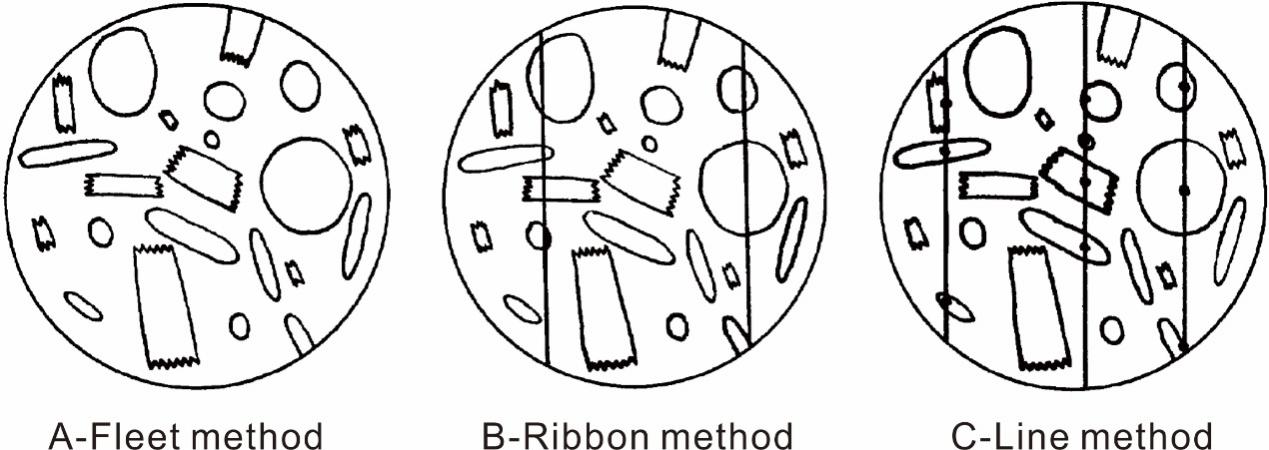
图1 早期碎屑统计采用的方法，分别为：Fleet method（统计所有颗粒）；Ribbon Method（统计两条线之间的颗粒）；Line Method（统计线上的颗粒）

小明：能具体解释一下吗？

沉积学家：点记法通过获得各类型颗粒的点数来代表其相对含量，分析岩屑的成分和比例。早期地质工作者采取如图1中的三种方法。然而该方法统计工作量大，而且统计的结果不能转化为碎屑组分的面积比。Glagolev和Chayes提出用网格进行多点计数的Glagolev-Chayes统计方法（图2D），该方法能够将面积比化作节点数的比例，因此统计的结果近似面积比。以Basu和Suttner为代表的学者提出，对中粒径砂进行碎屑统计才具有代表性。这种“窄粒径”范围选择性统计广泛受到质疑。由Gazzi和Dickinson提出，并由Ingersoll对其系统总结的Gazzi-Dickinson统计法（图2C），对“窄粒径”碎屑统计方法提出了质疑，并明确指出不需要对样品粒径进行筛选，对同一样品不同粒径的颗粒进行统计，结果更集中，而传统方法更分散 (Ingersoll et al., 1984)。

早期面积法采用标准卡片对比来近似估计颗粒的面积，然而这种方法受个人因素影响大，所估计的结果也不够准确。近年来，随着图像分析技术的迅速发展，一些地质工作者利用ImageJ和Photoshop等图像分析软件精确计算显微图片中各颗粒类型的面积(Grove et al., 2011; Zhang et al., 2014)，使得获得颗粒面积成为了可能（图2B）。

图2  目前四种常用的碎屑统计方法示意图。A-全颗粒统计法；B-全面面积统计法；C-Gazzi-Dickinson统计法；D-Glagolev-Chayes统计法

小明：停，STOP! 这么多种方法，你让我选哪种呢？

沉积学家：我们做了个对比实验，也许对你选择哪种方法统计有帮助。

选用两个现代河流砂样品，对同一样品采用四种方法进行统计，对比统计结果的差异性。统计结果显示，颗粒法与Gazzi-Dickinson方法统统计结果有较大的偏差，Glagolev-Chayes方法与全面积法统计结果近似，颗粒法与面积法统计结果的偏差最大（图3）。

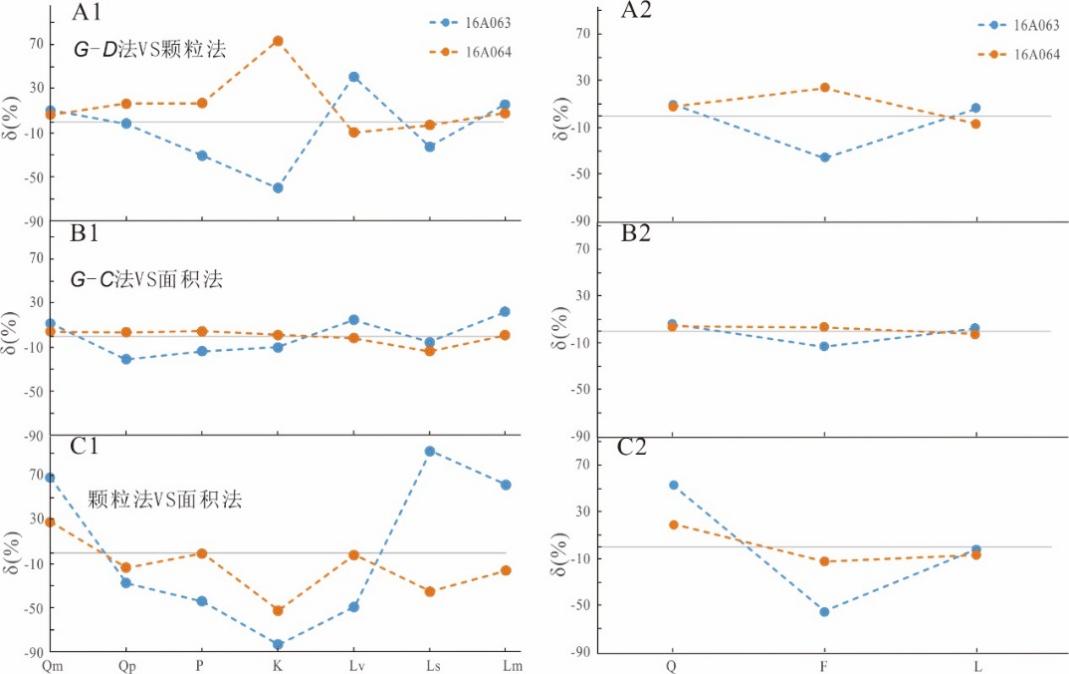
图3  四种不同的方法差异对比图。

（A1，A2）δ(%)= (G-D法－颗粒法)/颗粒法，表示以全颗粒法统计结果为标准，用Gazzi-Dickinson方法与全颗粒法统计结果作标准偏差；（B1，B2）δ(%)= (G-C法－面积法)/面积法，表示以全面积法统计结果为标准，Glagolev-Chayes法与全面积法统计结果作标准偏差；（C1，C2）δ(%)= (颗粒法－面积法)/面积法，表示以面积法统计结果为标准，全颗粒法与全面积法统计结果作标准偏差。全颗粒法=颗粒法，全面积法=面积法，Gazzi-Dickinson方法=G-D法，Glagolev-Chayes方法=G-C法

我们还基于Matlab进行了以上四种方法的模拟统计，与实际统计结果时一致的。补充统计样品不足的问题。

小明：我还是不明白要选用哪种方法统计

 沉积学家：用一句话来概括，要想获得砂或砂岩不同组成的物源信息，建议采用Gazzi-Dickinson统计法；要想获得砂或砂岩不同组成的通量（体积或者面积），建议采用面积法或者采用Glagolev-Chayes统计法。

小明：好的，明白了，那我要统计多少颗呢？

沉积学家：将碎屑统计认为是抽样统计，对于随机分布的总体，按照绝对精度决定样本量n的公式为：

n=(μ_1-α/2)²S²/［d²+(μ_1-α/2)² S²/N］

其中α为显著性水平；μ_1-α/2是N(0, 1)分布的1-α/2分位数；S²为总体方差，S²≈P(1-P)；d为绝对精度（绝对误差）；N为样品总数，P为颗粒百分比(Wald and Wolfowitz, 1944; 孙山泽, 2007 )

当α取0.05时，达到置信度为1-α=95%，此时μ_1-α/2=1.96；当P取0.5时，有最大总体方差0.25，d为绝对精度即绝对误差，一般取5%。可得到随着颗粒百分比的含量的增加，以及总体数量N的增加，所需抽样的样本容量曲线（图4）。

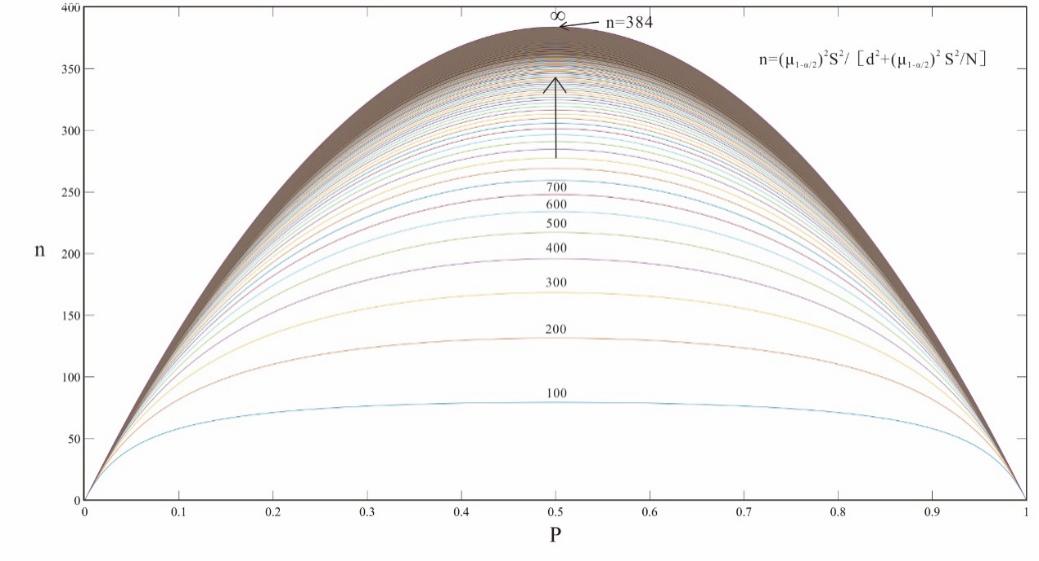
图4  碎屑统计数量参考图（出处）。不同颜色的曲线为样品碎屑颗粒总数，以100为公差递增；横坐标P为某种颗粒类型的百分含量，纵坐标n为需要统计的数量

所以对任意的样品，抽取的样本量达到384以上时，达到95%的置信度。

这个理论计算的数量是否符合实际样品的统计呢？

将样品16A063和16A064采用颗粒法和面积法统计的统计结果以10为公差的累积计算，将含量＜5%的颗粒类型与相似参数进行合并，共分为5类。以最终统计的结果作为标准，将其它各数量的统计结果与该标准求偏差（图5）。

总体而言两个样品在统计390颗以上时，各类型的统计结果与最终统计结果的偏差较小，且较为恒定，个别偏差依然较大的与颗粒含量较低有关。

所以理论计算出的384颗与实际统计结果相一致，且该统计数量不受颗粒分选的影响，是一个可行的统计数量。

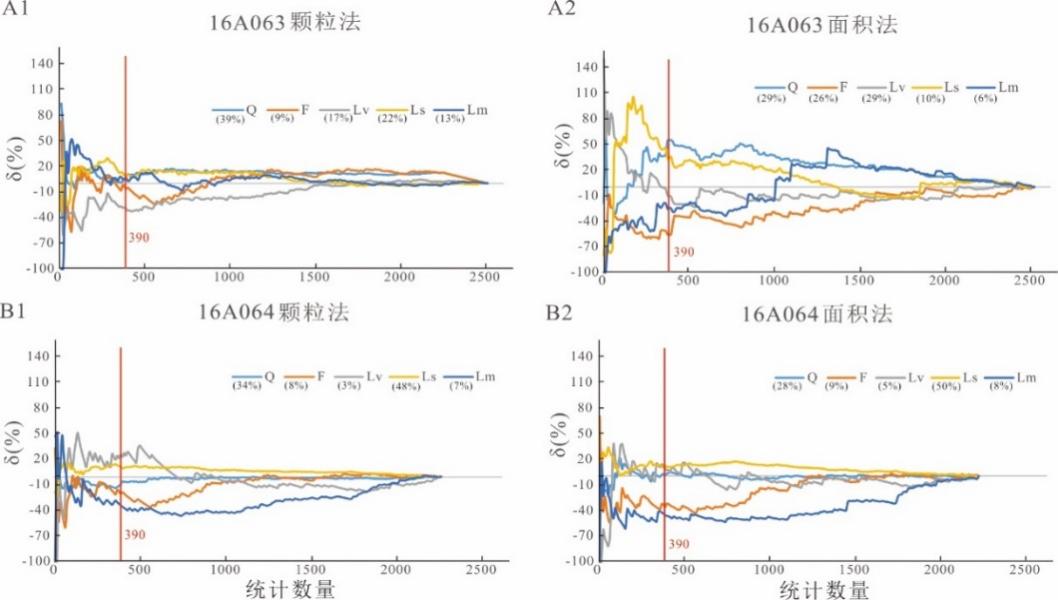
图5  样品16A063与16A064同时采用颗粒法和面积法统计结果，以10为公差累积统计

小明：明白了，那就是说，我只需要统计384颗以上就可以了是吧！

沉积学家：是的，但是我们通常会统计更多一些，现今大多数学者一个薄片统计400颗颗粒的做法是合理的。

小明：明白了，谢谢老师！

本文作者系南京大学地球科学与工程学院硕士研究生。本文属作者认识与理解，相关问题交流可通过邮箱MG1929006@smail.nju.edu.cn与本人联系。更多详情，请参考以下文献。

参考文献：

[1]  Ingersoll R V, Bullard T F, Ford R L, et al. The effect of grain size on detrital modes: a test of the Gazzi-Dickinson point-counting method[J]. Journal of Sedimentary Petrology, 1984, 54, 103–116.

[2]  Wald A, Wolfowitz J. Statistical tests based on permutations of the observations[J]. The Annals of Mathematical Statistics, 1944, 15(4): 358-372.

[3]  Grove C, Jerram D A. jPOR: An ImageJ macro to quantify total optical porosity from blue-stained thin sections [J]. Computers & Geosciences, 2011, 37: 1850-1859.

[4]  Zhang X, Liu B, Wang J et al. Wu S. Adobe photoshop quantification (PSQ) rather than point-counting: A rapid and precise method for quantifying rock textural data and porosities [J]. Computers & Geosciences, 2014, 69: 62-71.

[5]  孙山泽. 抽样调查[M]. 北京：北京大学出版社，2007: 1-169.

[6]  董小龙，胡修棉，郭荣华，等．河流砂碎屑统计方法的对比实验研究[J]．沉积学报. https://doi.org/10.14027/j.issn.1000-0550.2021.099.