Progress and Prospects for Simulating Deep-water Gravity Flow Sedimentation

深水重力流是由重力驱动的^[1]，富含陆源碎屑的高密度流体^[2⁃3]，其携带的大量陆源碎屑在海底形成了地球上最大的复合沉积体^[4]，储存了全球35%的深水油气资源^[5]。现代海底监测显示，一期重力流事件可以携带超过150 km³的沉积物，以19 m/s的速度运行^[6]，对海底通信电缆及输油管道安全具有重大威胁^[7]。此外，深水重力流可以将大量陆源和海洋的有机碳输送至深水环境，在地质时间尺度上实现碳循环的中转和汇聚，有助于调节全球气候^{[4, 8⁃9]}。深水重力流具有典型的事件性特征，可以由火山喷发^[10]、地震活动^[11⁃12]、风暴^{[13- 14]}、洪水^[15⁃17]等多种作用触发。因此，重力流沉积也是地质历史时期洪水、火山或古地震等极端事件的有效记录者。最新研究指出，重力流也可不需要明显的外部触发机制^[18]，超低浓度（沉积物含量约0.07 kg/m³）的羽流自加速同样可以形成深水重力流^[19]，因此深水重力流的发生可能远比想象中更为频繁。

自1888年Forel^[20]报道日内瓦湖密度流以来，重力流研究迅速发展。时至今日，众多学者在重力流的沉积类型^[21⁃24]和沉积模式^[25⁃26]等方面取得了长足的进步。Middleton et al.^[21]根据颗粒支撑机理将重力流划分为碎屑流、颗粒流、液化流和浊流4种类型；Lowe^[22]依据流体流动状态，将浊流进一步分为高密度浊流和低密度浊流；Talling et al.^[23]根据流体黏土含量和流变学特征将碎屑流分为黏性碎屑流和非黏性碎屑流（砂质碎屑流）；Baas et al.^[24]发现随着重力流中黏土含量的增大，会出现一种介于牛顿流体和非牛顿流体之间的过渡型流体；Walker^[25]结合古代露头和现代实例，提出了经典的海底扇模式；Shanmugam^[26]总结了斜坡环境下滑塌型重力流的演化过程，建立了以碎屑流为主导的斜坡扇模式。近年来，由盆外洪水入海（湖）形成的洪水型重力流（异重流）引发了新一轮的重力流研究热潮^[27⁃29]。事实上，重力流沉积过程极为复杂，触发机制^[16,30⁃31]、流体性质^[23,32]、先存地貌^[33⁃36]等多种因素都可能导致沉积产物的巨大差异，经典的沉积模式并非“万能模板”，新的问题要求研究者们采取针对性的研究手段，提出更合理的解释。

传统的重力流研究主要依靠野外露头、钻井、地震等手段，以静态沉积现象分析为基础从而对沉积产物的形成过程^[37⁃39]、影响因素^[40⁃43]、分布模式^[26,44]进行解释。现场观测能够直接获取真实尺度下的动态数据，但限于深水重力流沉积事件的偶然性和发生场所的特殊性，现场流体监测难度较大。相比之下，沉积模拟实验能够在不同尺度下通过控制边界条件，再现各种自然环境中的沉积过程和水动力特征，是理解和认识深水重力流沉积动力过程和沉积规律的最重要手段。本文在国内外深水重力流沉积模拟实验相关文献调研的基础上，系统梳理重力流沉积模拟发展历程，从重力流沉积模拟的实验理论、实验技术、关键应用和最新进展等多个方面展开论述，以期能够推动国内重力流沉积模拟研究，更好的服务于深水油气勘探。

重力流沉积物理模拟实验起源于20世纪初，至今已有100余年的历史。根据不同时期物理模拟实验的主要关注点，可以将其分为以下4个阶段（图1）。

Figure 1.  Phase division and main progress of physical and numerical simulation of deep⁃water gravity flow deposits

1960年之前，沉积现象观察阶段。1914年，Gilbert^[45]通过水槽实验观察到了类似牵引毯（traction carpet）的构造，将其称为跃变层（saltation layer），此外他还观察到沉积物浓度自下而上逐步递减的现象。Kuenen et al.^[46]于1950年开展了第一次浊流实验，认识到浊流在深海沉积物输运的重要性，提出递变层理是浊流的重要标志，促进了浊流理论的诞生，被誉为“沉积学研究的一场革命”。

1960—1980年，沉积底形及沉积构造研究阶段。Simons et al.^[49]基于明渠流水实验讨论了底床粗糙度对冲积河道底形的影响，总结了不同流态（上部流态、下部流态和过渡态）的底形特征。尽管该研究目标并非是针对深水重力流沉积，但作为首次系统性的水槽底形实验研究，激发了重力流沉积底形的水槽研究热潮；此后，Middleton^[50]开展了涌浪型重力流模拟实验，将涌浪型重力流分为头部、体部和尾部，还观察到了高浓度浊流的粗尾递变（coarse-tail grading）构造。

1980—2000年，沉积机理及沉积过程研究阶段。Southard et al.^[52]提出密度流自悬浮（auto suspension）这一概念，讨论了粒度和坡度对沉积物自悬浮能力的影响；Postma et al.^[54]通过水槽实验研究了高密度浊流的分层性，发现高密度浊流实际包含下部塑性层流状的碎屑流和上部稀性浊流两种性质各异的流体；Kneller et al.^[55]再现了浊流在封闭盆地边缘遇到障碍物后的反射过程，提出了边缘斜坡上内孤立波（internal solitary waves）的形成机制；Mohrig et al.^[57]基于模拟实验证实了滑水作用（hydroplaning）的存在，为水下碎屑流和滑块在低坡度下的长距离搬运提供新解释；Marr et al.^[58]利用水槽实验讨论了黏土矿物对水下碎屑流流体演化的控制作用，研究发现不同类型的黏土矿物形成碎屑流的下限浓度差异较大，蒙脱土最低仅需0.7%的质量分数即可形成碎屑流，而高岭土则需7%。

2000年至今，沉积—地貌动力学定量研究阶段。高精度监测仪器的快速发展，使得深水重力流水槽实验逐渐转向定量阶段。Ilstad et al.^[32]基于不同黏土含量条件下重力流模拟实验，讨论了黏土矿物含量对重力流流体类型、流速剖面及沉积厚度分布的影响；Lamb et al.^[61]基于异重流沉积模拟实验指出平均深度的异重流流速与河流洪水流量变化相关性较差，而沉积物中的粗细颗粒一定程度上可以反映多重流动的速度波动和河流流量大小；de Leeuw et al.^[64]认为早期堤岸沉积的形成可能是受控于平坦斜坡上的浊流自生过程，而非浊流漫溢产物；Pohl et al.^[66]提出了新的流动机制——流动松弛用以解释海底水道—朵体过渡带大量沉积底形的发育机制；Miramontes et al.^[67]通过水槽实验再现了重力流—等深流交互体系中重力流水道的单向迁移过程，总结了等深流流速对堤岸沉积的影响。中国方面，刘忠保等^[59]重现了陡坡带砂质碎屑流的形成过程，指出斜坡长度、基准面的相对变化控制了碎屑流沉积体的发育规模和发育部位；鄢继华等^[60]模拟了不同触发条件下三角洲前缘浊积砂体的形成过程和分布规律。

物理模拟实验的关键是要解决模型与原型之间相似性的问题，实验过程中必须遵从相似性理论。模型与原型之间必须遵守的相似理论包括几何相似、运动相似及动力相似^[70]。

几何相似是保持实验模型的几何形状、大小与实际原型相似；同时，实验样品的物理和力学特性，如密度、粒度、磨圆度等，应与原型相匹配。运动相似要求实验过程中流体运动状态和实际情况相似。此外，保持模拟实验与实际地质过程的时间尺度相似，有助于确保实验结果能够准确反映实际流体流动行为。

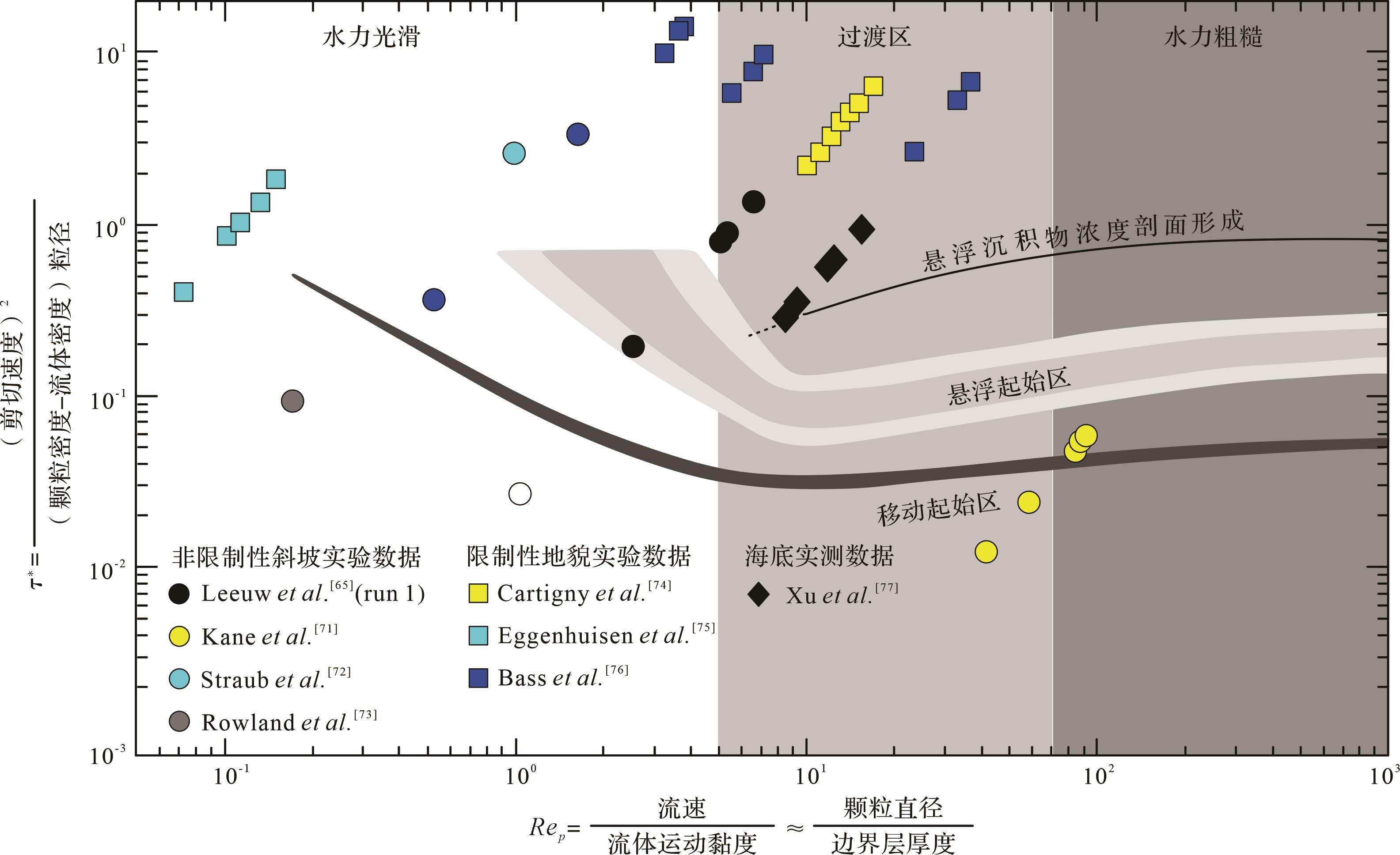
动力相似要求实验中液体和颗粒之间的流动和相互作用的动力行为与实际流体的动力行为相似。经典的浊流模拟实验用弗劳德数（Fr，表征为流体动量和重力之比）以及雷诺数（Re，表征为动量和黏性力的比值）描述浊流运动的动力特征，实验过程中一般保证Fr与自然值接近，Re高于层流的阈值以保证紊流状态。然而，该方法忽略了对颗粒运动状态的描述，不能确保颗粒主要以悬移态运动。de Leeuw et al.^[64]用希尔兹数（τ^*，湍流剪切应力与重力的比值）和颗粒雷诺数（Re_p ）描述颗粒运动状态，并结合重力流海底监测和水槽实验资料^[71⁃77]，建立颗粒运动机制图版以约束重力流沉积模拟实验中的动力边界条件，从而提高实验结果的可信度和可靠性（图2）。

Figure 2.  Motion state diagram of particles (modified from reference [64])

重力流物理模拟研究中实验数据的采集主要可分为三类：水下流速测量、悬移质浓度测量和沉积地貌扫描。水下重力流的速度场是物理模拟实验最关注的参数之一。目前水槽实验中主要的测速方法可分为多普勒测速和粒子成像测速两类，其中多普勒测速法依据测量原理和测量范围又可分为激光多普勒测速（LDA）、超声多普勒测速剖面（UDVP）和声学多普勒测速（ADV）^[78]。LDA侧重于高空间分辨率的点测量，ADV则注重于高时间分辨率的瞬时三维点测量，UDVP可以实现垂直剖面的流速监测。粒子成像技术（PIV）利用高速相机捕捉示踪粒子的运动信息，可通过计算机技术生成高精度流场数据，但仅适用于低浓度二维水槽或重力流沉降实验^[78]。此外，悬移质浓度测量、沉积地貌扫描等技术也是重力流沉积物理模拟实验的关键手段，对重力流定量化研究具有重要意义。

20世纪中期以后，重力流沉积模拟迅速发展，以美国、英国、荷兰等发达国家为代表，全球各大科研机构相继建立了一批重力流沉积模拟水槽实验平台（表1）。国外重力流物理模拟水槽实验类型多样，研究内容广泛，在重力流流体结构、沉积过程、砂体分布等方面涌现出一批代表性成果。如杜伦大学的Matthieu Cartigny团队对超临界重力流底形和水跃作用进行了深入研究^[63,80]；乌德勒支大学的Joris Eggenhuisen团队基于水槽实验对浊流与深水地貌之间的作用机制提出了新的见解^{[66⁃67,74⁃75]}；Jaco Baas团队在利兹大学期间专注于细粒黏性重力流物理特性和沉积特征^[24,76,88]；Gary Parker团队在明尼苏达大学期间针对浊流的沉积物输运过程和形态动力学开展了一些基础性研究^[89⁃92]。

20世纪70—80年代长春地质学院和中科院地质所率先揭开了中国沉积物理模拟研究的序幕。随后，由于国内油气勘探的需求，长江大学建立了CNPC湖盆沉积模拟实验室。中国石油大学（华东）、中国地质大学（北京）等也开始各自筹建沉积物理模拟实验室。当前我国的重力流沉积物理模拟研究主要关注于砂体发育特征及分布规律^[59,93⁃95]，对沉积动力过程和地层动力研究比较缺乏，同时相应的监测设备较为落后，定量化与自动化程度较低。由于逐渐认识到物理模拟实验对沉积学基础理论研究的重要性，目前中国石油大学（北京）、成都理工大学等高校正在筹建现代化沉积物理模拟实验平台。

沉积物组成是决定流体性质的最基本参数，流体的沉积物浓度、砂泥比、黏土类型、颗粒大小等对流体性质均有不同程度的影响。

沉积物浓度直接决定了重力流流体类型，随着沉积物浓度的降低，碎屑流总是趋于向浊流转化。一般认为，高密度浊流的体积浓度应大于6%或流体密度大于1.1 g/mL^[46]；当沉积物体积浓度达到25%时，流体紊流受到完全抑制最终转化为碎屑流^[26]。沉积物颗粒大小对流体类型与运动状态同样具有重要影响。Elerian et al.^[85]发现较大的颗粒粒径会显著降低浊流的锋面速度和搬运距离，而颗粒浓度一定程度上可以中和颗粒尺寸对浊流运动的影响，浊流浓度足够高时，颗粒尺寸对浊流运动的影响已经微乎其微。此外，粗颗粒相较于细颗粒更易形成碎屑流，且搬运距离更远^[59]。黏土矿物和有机质作为流体内聚力的直接来源，能够有效的抑制浊流的紊流性质，使流体向层流性质的碎屑流转变^[23]。最新研究发现，浊流与碎屑流之间存在着流体性质介于紊流和层流之间的过渡型流体^[96]。随着黏土矿物的增加，浊流会逐步转化为紊流增强过渡流、上过渡塞流、准层状塞流等过渡型流体，并伴随独特的底床类型^[97⁃98]。然而，不同类型的黏土矿物由于物质组成和分子结构的差异，其吸水膨胀能力显著不同，蒙脱土的亲水性可达高岭石的60倍^[99]。水槽实验指出蒙脱土最低仅需0.7%的质量分数即可形成碎屑流，而高岭土则需7%的质量分数^[58]。

经典的海底扇模式由深水水道、堤岸、朵体以及水道—朵体过渡带等组成^[25,100]。重力流通过其强大的侵蚀搬运能力塑造不同的沉积单元，沉积单元又因其内部的形态差异反作用于流体运动过程，两者之间的相互作用是重力流研究的重点内容。

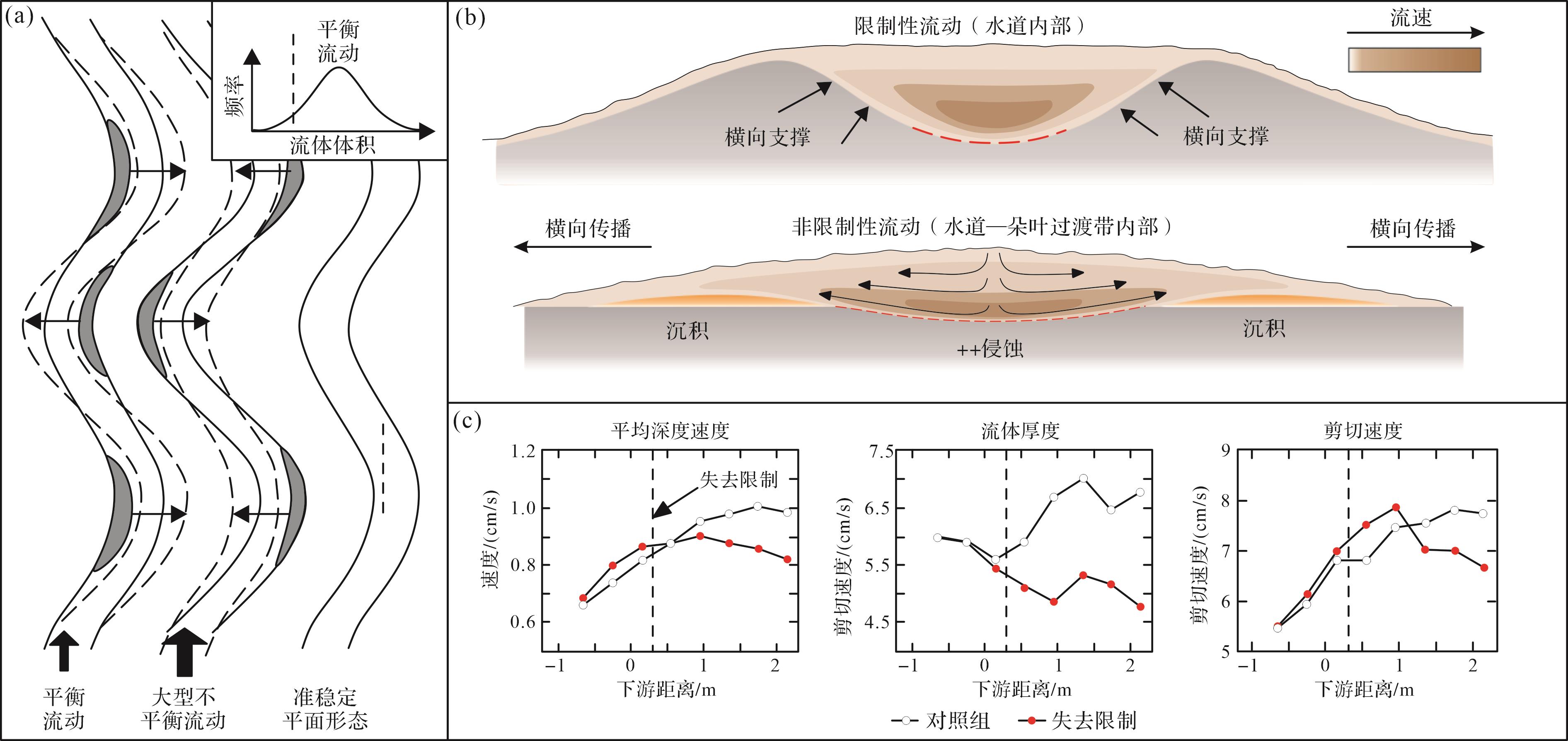
深水水道是深海沉积物输送的主要途径^[101]，其内部充填物记录了源区古气候变化^[102]，同时也是良好的油气储层^[103]。Keevil et al.^[104]通过弯曲水道模拟实验指出深水水道的次级流动对沉积物分配具有重要影响，深水水道处的次级流动有利于堤岸外侧粗粒沉积物堆积。Kane et al.^[71]认为深水水道中的大型不平衡流动导致水道外弯处沉积大量泥沙，使水道短暂变直，进而增强了深水水道的平面稳定性，使其不易像陆上河道频繁发生截弯和决口（图3a）。

Figure 3.  Sedimentary⁃hydrodynamic characteristics of gravity flow in different sedimentary units

水道—朵体过渡带是连接深水水道和深海盆地的过渡性区域。当浊流离开水道进入深海盆地，流体失去水道的侧向限制发生横向扩散，进而增加了水体的整体摩擦，导致流体减速和悬浮沉积物沉降，并在水道末端堆积形成朵体复合体。然而，多地海底观测在水道—朵体过渡带发现的冲刷场（scour field）构造^[105⁃108]，表明水道—朵体过渡带可能并非以沉积作用为主。Komar^[109]认为冲刷场的形成是由于浊流失去限制性后，流体从超临界流向亚临界流转变，伴随而来的水跃作用增强了流体的侵蚀能力。Pohl et al.^[66]在室内水槽实验中并未发现水道—朵体过渡带的水跃作用及其伴生的流厚突然增加现象^[76]。结合实验结果，Pohl et al.^[66]提出流动松弛机制用来解释冲刷场现象（图3b）。当浊流离开水道后，流体失去横向限制向两侧扩散，流速整体降低，但流体厚度减薄的同时也导致浊流头部最大流速深度相应降低，进而导致靠近底床的流体剪切速度增大（图3c），由此增强了浊流的基底剪切能力，有利于冲刷场的形成。

深水环境主要发育重力流和等深流两种沉积物输送机制。重力流是一种瞬时、高能的事件性流体，而等深流则是受地球自转作用力影响而产生的持续存在的低能流体。等深流可以改造先存或正在沉积的重力流水道，形成等深流—重力流混合沉积体系^[110⁃112]。

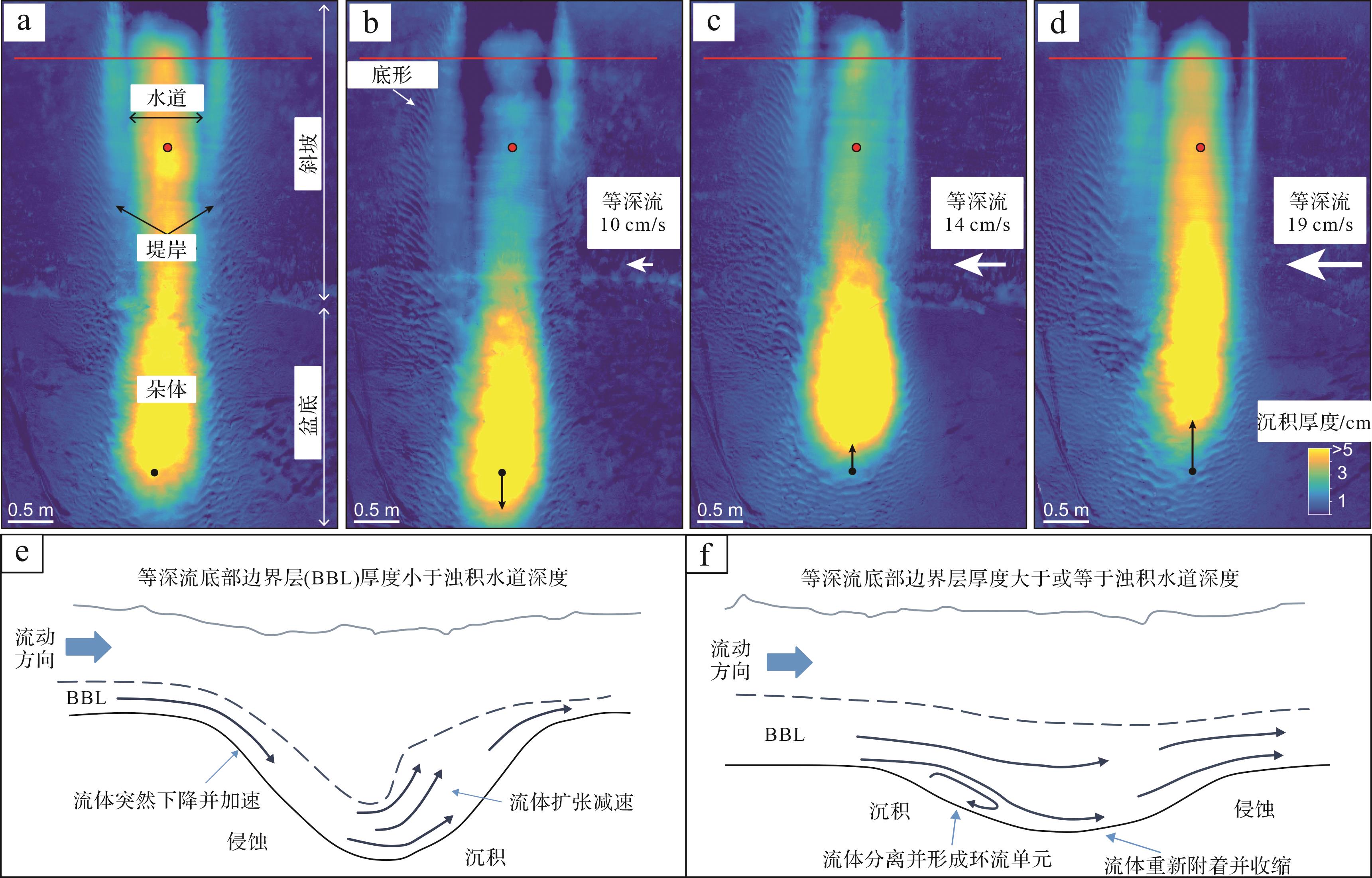
Miramontes et al.^[67]通过水槽实验再现了重力流水道的单向迁移模式。当浊流和等深流同时处于活跃时期，一定强度的等深流可以使浊流发生偏移和不对称溢出，在盆地下游形成不对称的堤岸系统。同时，等深流流速对堤岸发育程度具有重要影响，流速越快，上游堤岸沉积越厚，下游堤岸沉积越宽，并导致水道向上游迁移（图4a~d）。Fedele et al.^[113]发现重力流水道的迁移方向取决于等深流流体底部厚度与重力流水道深度的相互关系。当等深流底部边界层厚度远小于重力流水道深度时，等深流会完全落入重力流水道，在水道上游处，流体加速下滑，造成侵蚀；下游处，流体减速爬升，并逐渐沉降，由此导致了重力流水道沿等深流流向反向迁移（图4e）；当等深流底部边界层厚度接近或大于重力流水道深度时，等深流底部边界层会在水道上游发生分离，等深流携带的物质就此沉降，流经水道下游时，底部边界层与上部等深流附着并收缩，并可能促进沉积物的改造和侵蚀，这种情况下重力流水道顺着等深流流动方向迁移（类似于沙丘迁移）（图4f）。

Figure 4.  Migration mode of gravity flow channel

超临界浊流是指密度弗劳德数（Fr_D）大于1的，可通过水跃作用转化为亚临界流的深水重力流^{[109,114⁃115]}。研究表明，超临界浊流与海底峡谷^[80,116]、深水水道^[117⁃118]、周期阶坎^[119]等海底地貌的形成密切相关。然而，由于其强大的侵蚀能力，超临界浊流留下的地质记录相对较少^[63]，导致人们对其理解仍然有限。

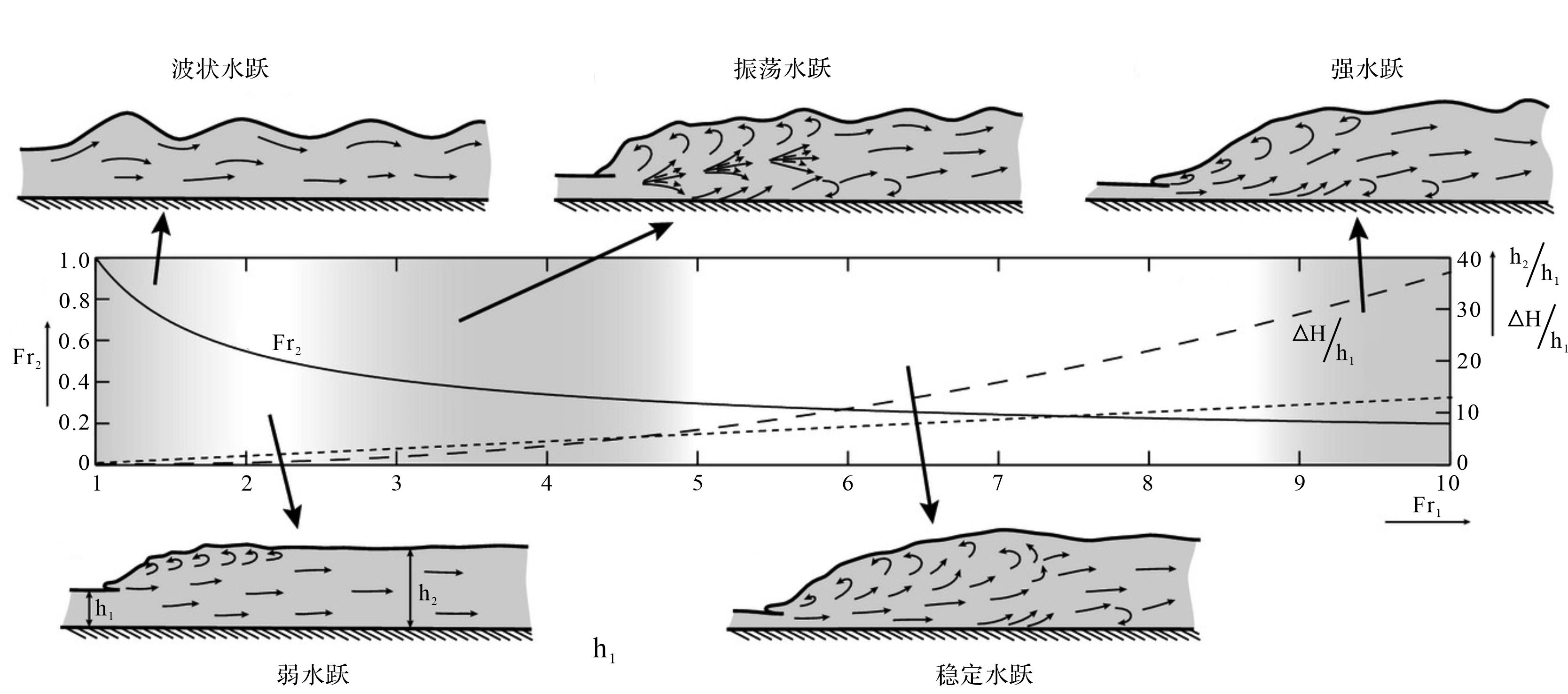
Sequeiros^[82]基于历年的水槽实验和现场观测数据指出当底床坡度大于0.5°时，浊流就具备了转化成超临界流的条件。随着弗劳德数的增大，超临界流底形依次向着逆行沙丘、不稳定逆行沙丘、冲坑和冲槽、旋回阶坎转变^[63]。其中逆行沙丘和旋回阶坎作为该过程的两大稳定单元，其沉积记录在海底观测中多有发现。水跃（hydraulic jump）作用是超临界流向亚临界流的突然过渡，其特征是流体厚度急剧增加，流速下降，流体能量大量损失。Cartigny et al.^[63]提出在不考虑流体或沉积物夹带的前提下，用共轭深度比（水跃前超临界流厚度/水跃后亚临界流厚度）来衡量水跃强度等级，将其分为波状水跃、弱水跃、振荡水跃、稳定水跃、强水跃五类（图5）。水跃作用的内部结构受控于共轭深度比，共轭深度比越大，水跃过程中的能量损失越大。

Figure 5.  Morphology and hydrodynamic structure of hydraulic jump (modified from reference [63])

Ono et al.^[87]通过水槽实验研究了涌浪型浊流中水跃作用对底床形态、粒度分选的影响。单期涌浪型浊流可以在一个旋回阶坎的迎流面下部形成多次冲刷，浊流的头部、体部和尾部可以在迎流面不同位置产生水跃，从而形成多期冲刷充填体，随着旋回阶坎向上游逐渐迁移，同时产生向上变细的沉积序列。该研究为海底旋回阶坎中含多重冲刷特征、向上变细的浊积岩序列^[120]提供了一种新的成因解释。

深水重力流数值模拟是通过数学方法来研究和预测重力流运动行为^[121]。其原理基于牛顿力学和流体力学的基本方程（包括质量守恒方程、动量守恒方程和能量守恒方程）^[78]。重力流数值模拟能够在多个尺度上再现重力流沉积演化过程，明确重力流流体动力参数的时空变化，还可以预测海底扇发育模式与构型样式，指导深水油气勘探。由于高浓度流体需要考虑颗粒之间的碰撞运动，极大程度上增加了运算的工作量，目前深水重力流数值模拟研究主要集中在低密度浊流领域。

1980年之前，经验公式和简化模型阶段。1845年，用于描述黏性不可压缩流体动量守恒的纳维—斯托克斯（Navier-Stokes，N-S）方程就此问世。虽然N-S方程理论上可以描述湍流在三维时空内的全部流动细节，但由于湍流瞬时运动的极端复杂性，基于N-S方程的直接数值模拟方法仍然极具挑战性。为了便于计算机求解，科学家们开始提出简化的计算模型。1952年，Kuenen^[47]首次运用切奇公式评估了1929年纽芬兰大浅滩的浊流事件^{。随后，Ellison et al.[48]提出了基于N-S方程简化的深度平均模型（Depth-averaged moded），该模型假设流体在垂直方向上的性质变化不显著，允许通过垂直积分来计算流体动力参数。Chu et al.[51]选取深度平均模型，并根据弗劳德数的变化，将浊流的运动过程分为流动建立、均匀流动、水力跳跃和流动衰减4个阶段。基于平均深度理论，Parker et al.[53]推导出描述浊流动力学的层平均运动方程，再现了浊流的自加速效应；此后，一些研究者开始将盒子模型[56,122]用于重力流数值模拟，并取得了较好的应用效果。事实上，浊流存在显著的分层结构[54]，平均深度模型只能描述浊流平面上的运动过程，而忽略了垂直方向上的运动，限制了计算结果的适用性。}

1980—2000年，二维混合模型阶段。1980年起重力流数值模拟理论迅速发展，形成了以雷诺平均数值模拟（Reynolds Average Navier-Stockes，RANS）、大涡模拟（Large Eddy Simulation，LES）、直接数值模拟（Direct Numerical Simulation，DNS）为主的3类模拟方法。其中RANS的核心思想是应用湍流统计理论，对N-S方程进行时间平均，从而计算得到时均流场数据^[123⁃124]。由于雷诺平均方程并不封闭，需要引入雷诺应力的平均模型^[83]。该法可以提供运动的平均物理量，满足大多数工程计算需求，但在处理强剪切（靠近墙壁或障碍物）以及低至中等雷诺数流动的区域时计算效果不佳^[125⁃126]。大涡模拟通过特定的滤波函数将湍流的瞬时运动分解为大尺度运动和小尺度脉动，大尺度运动通过N-S方程直接求解，小尺度脉动通过特定的湍流模型进行简化计算^[127]。该方法能够得到流体瞬时运动的脉动量，但其计算量也远高于RANS法^[128]。此外，为了获取更高精度的模拟结果，一些研究者开始采用直接数值模拟求解湍流方程的全部参数，但由于湍流运动的复杂性，需要极高的计算资源，且不适用于较高雷诺数的浊流运动模拟^[69,129]。

2000年至今，高分辨率三维数值模拟阶段。随着计算机处理能力的显著提升，科学家可以进行高分辨率的三维重力流数值模拟。这使得对复杂地形、多粒度分布以及流体—固体相互作用等的高精度模拟成为可能。如Howlett et al.^[130]利用数值模拟技术研究非限制性浊流对海底褶皱地貌的响应机制，观测到了浊流的开尔文—亥姆霍兹不稳定性和水跃现象；Abd et al.^[131]模拟了尼日尔三角洲大陆斜坡的海底浊流运动，预测了浊流演化过程和不同粒级颗粒的空间分布。此外，机器学习和人工智能技术被逐渐引入到重力流数值模拟中^[132⁃134]。这些技术有助于优化模型参数，识别模式，甚至预测未知条件下的沉积过程。

重力流数值模拟起源于20世纪中期^[48]，作为一种重要的工程和科学研究手段，被广泛用于海洋工程灾害评估^[135]、河流泥沙运移^[136⁃137]、油气勘探^[138⁃139]等领域。根据不同的应用需求和模拟目标，众多研究机构或商业公司开发了各具特色的重力流数值模拟平台。

Flow-3D是一款由美国Flow Science公司开发的商业计算流体动力学（Computational Fluid Dynamics，CFD）软件。它基于有限体积法建立三维模型，采用多相漂移通量流法预测浊流运动。Flow-3D将泥沙扩散视为连续相，计算流体空间体积浓度。Flow-3D可以监测浊流在时间和空间上的连续流动特征，包括流动密度、沉积物浓度、粒度离析、空间平均速度场、内部剪切应变率（湍流强度）、动态黏度和底部剪切应力等^[140]。

Fluent软件起源于谢菲尔德大学的Boysan et al.^[141]开发的CFD代码，后被ANSYS公司收购，并整合为ANSYS Fluent。目前，Fluent已成为应用最为广泛的商业CFD软件之一。Fluent软件基于有限体积法，将流动区域离散化为有限体积，并通过求解连续方程、动量方程和能量方程等基本方程来模拟浊流的流动和传输过程。Fluent软件支持GPU并行计算，能够显著降低浊流数值模拟的计算时间^[142]。

Delft3D是代尔夫特理工大学开发的开源流体动力模拟软件。该软件基于泥沙水动力方程，可以实现沉积物输运和地貌演变的三维模拟。Delft3D侧重于河流、三角洲、浪控等的沉积模拟，同时也可用于预测深水重力流的运动过程和水动力特征^[143⁃144]。

CATS（The Cellular Automata for Turbidite Systems）是由法国石油研究院开发的一款用于模拟浊积岩储层的结构和空间分布的工业软件。该软件基于势能、动能平衡和扩散原理，以临近单元（元细胞自动机）之间的局部规则对给定地形的浊流流动进行建模。CATS软件无需求解复杂的水动力方程，计算量小，模拟时间短，对浊积体内部结构刻画效果较好^[138]。

Sedsim（Sedsim Forward Stratigraphic Modelling）软件是由斯坦福大学在20世纪80年代开发的三维地层正演模拟软件。Sedsim软件基于简化的N-S水动力学方程，能够在地质和工程时间尺度上模拟地层或盆地形成过程。Sedsim软件可以模拟构造、海平面变化、气候等因素影响下的多类型沉积过程，广泛应用于油气勘探预测中^[145]（表2）。

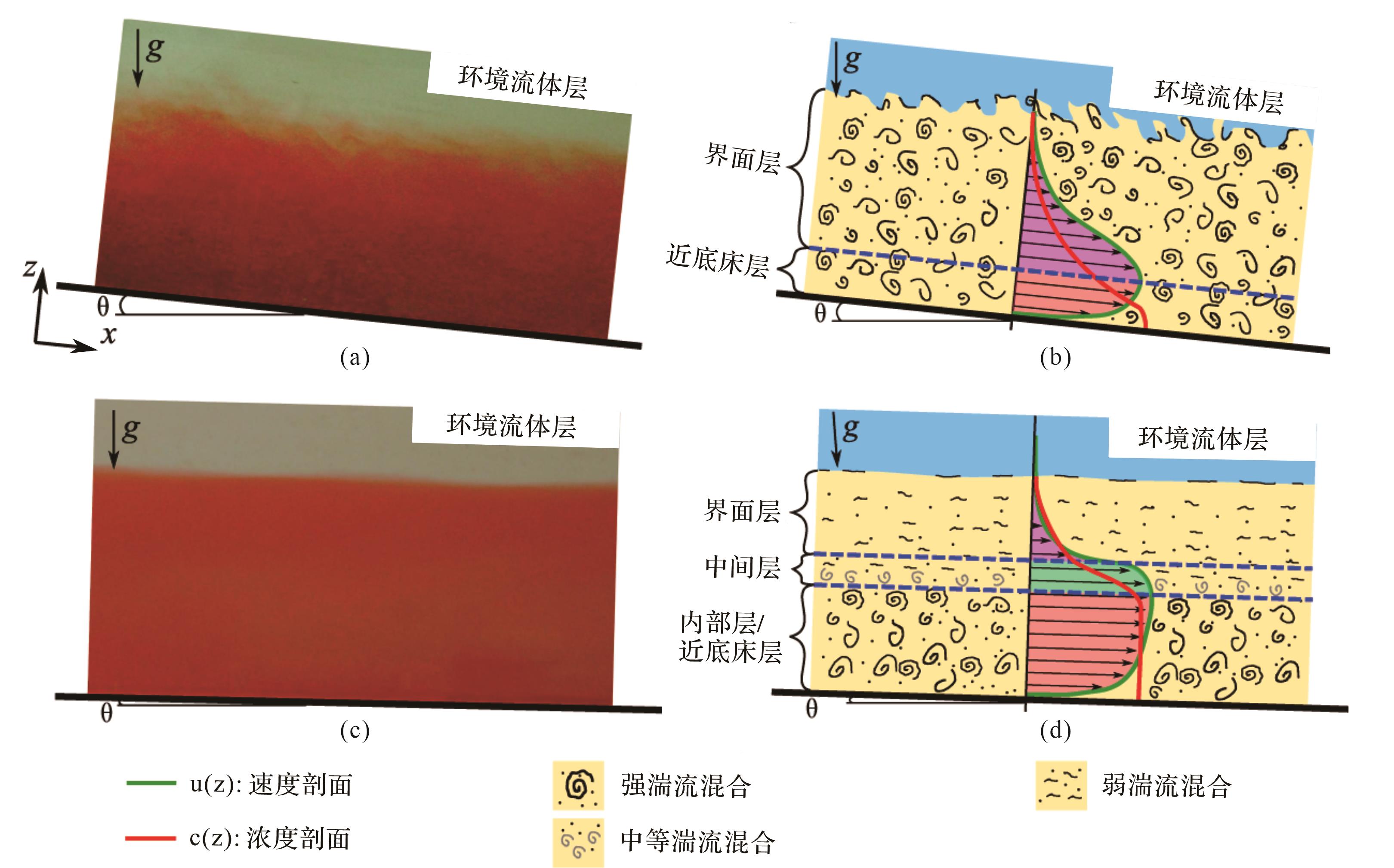
三维数值模拟可从不同尺度、不同角度系统对比分析浊流的动力学特征。模拟过程中可以对关键参数进行连续监控，分析其变化所伴随的沉积响应。Salinas et al.^[68]基于重力流数值模拟发现，超临界浊流具有近床层和界面层组成的双层结构，两层流体都表现为高度湍流特性，垂向最大流速出现在近底床层和界面层的交界处（图6a，b）；相比之下，亚临界浊流（体部）自下而上由近床层、中间层、界面层组成。其中仅近床层具有高度湍流性质，该层沉积物具有良好的混合，向上流体雷诺数减低，至界面层时已与环境水体层出现明显的光滑界线^[68]（图6c，d）。研究表明，亚临界流体的三层结构可能与海底水道中浊流的超长体部的形成有关^[68]。

Figure 6.  Fluid structures: (a, b) supercritical structure; (c, d) subcritical structure (modified from reference [68])

密度弗雷德数是区分超临界浊流与亚临界浊流的关键参数，通常认为超临界浊流的密度弗劳德数大于1，亚临界浊流的密度弗劳德数小于1。Huang et al.^[146]提出重力流的临界密度弗雷德数不一定是一个恒定值。根据周围流体的夹带程度和重力流的密度变化，重力流的临界密度弗雷德数存在3种情况，大于1，不存在或小于1。此外，传统观点认为异重流入水后，沉积物颗粒的不断沉降会降低异重流的密度，导致异重流的搬运距离较短。然而最新研究显示，沉积物颗粒—盐的扩散率差异可以使异重流转为含盐浊流，异重流损失沉积物的同时会从环境水体（海水）中吸收相应的盐分，从而维持异重流的密度稳定，并能够搬运至相当长的距离^[147]。

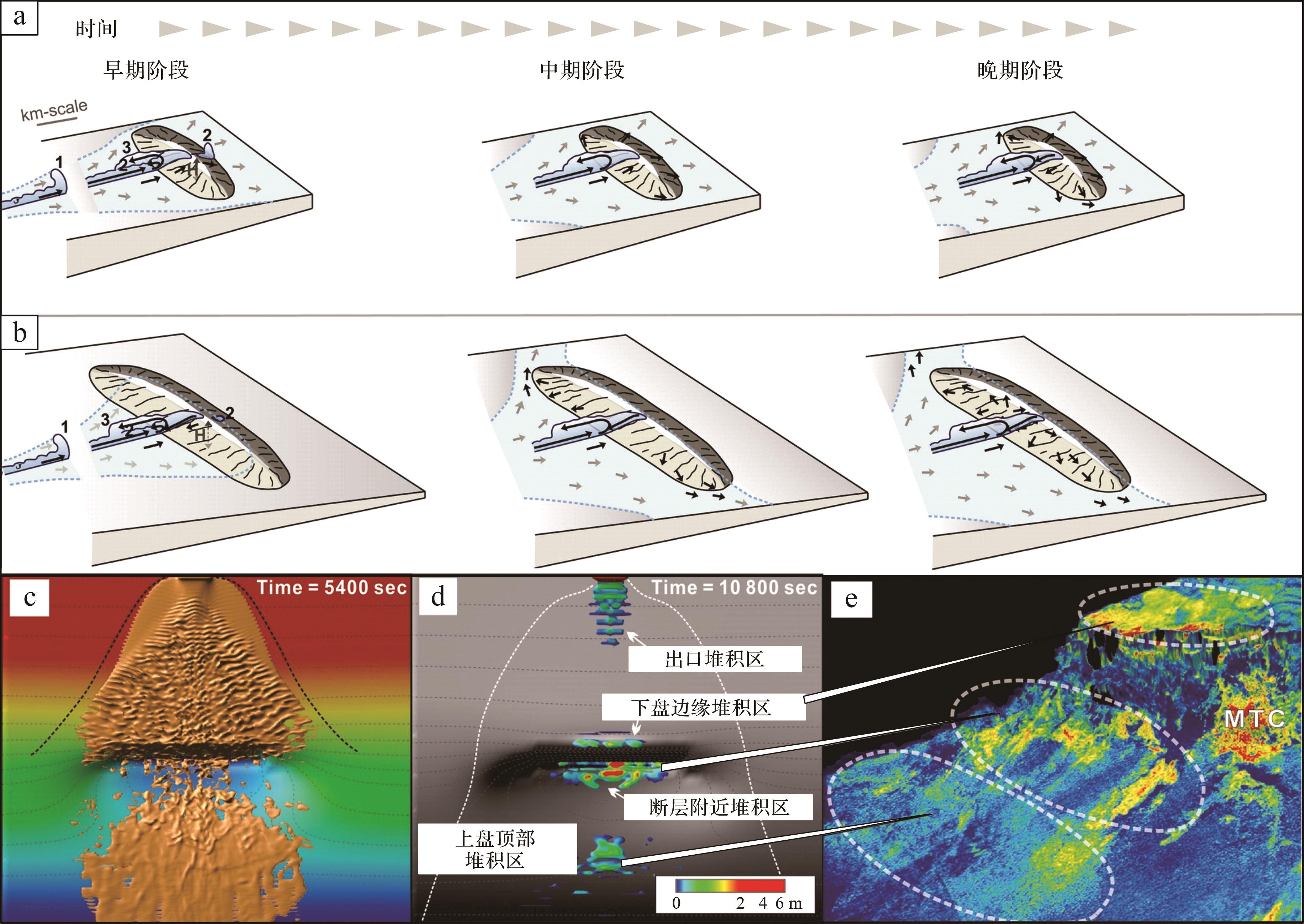
数值模拟可以提取地下地貌数据，构建多样化的地质模型，再现深水地貌与重力流沉积的交互过程，并揭示有利沉积体的分布规律。褶皱和断层作为挤压构造背景下产生的典型地貌，广泛存在于陆相断陷湖盆和深海构造活跃带，深刻控制着海底沉积物的运输和沉积^[34]。Howlett et al.^[130]通过数值模拟总结了非限制性浊流对褶皱地貌的响应模式。根据褶皱地貌与浊流的相对大小，可分为大褶皱小浊流和小褶皱大浊流两种模式（图7a，b）。当褶皱地貌远小于浊流体积时，浊流主体能够越至褶皱后翼，发生水跃作用导致浊流减速、颗粒沉降，在褶皱后翼前缘、后翼反斜坡、褶皱前翼形成明显的沉积区；当褶皱地貌远大于浊流体积时，浊流主体在褶皱前翼减速沉积，少量低密度流体越过褶皱后翼并发生水跃作用。Ge et al.^[65]通过数值模拟揭示了真实尺度下浊流流经正断层地貌时的沉积过程和沉积模式（图7c~e）。研究发现该模式与传统的斜坡扇模型^[26]存在较大差异：受断层地貌影响，砂体成斑状分布，自上而下可分为四个主要沉积区：浊流出口堆积区、下盘边缘堆积区、断层顶部堆积区以及上盘顶部堆积区。在浊流的沉积过程中，开尔文—亥姆霍兹界面的不稳定性引起了流速大小和泥沙浓度的三维波动，进而调节了沉积物的分配。

Figure 7.  Sedimentatary process and gravity⁃flow deposition in complex landforms

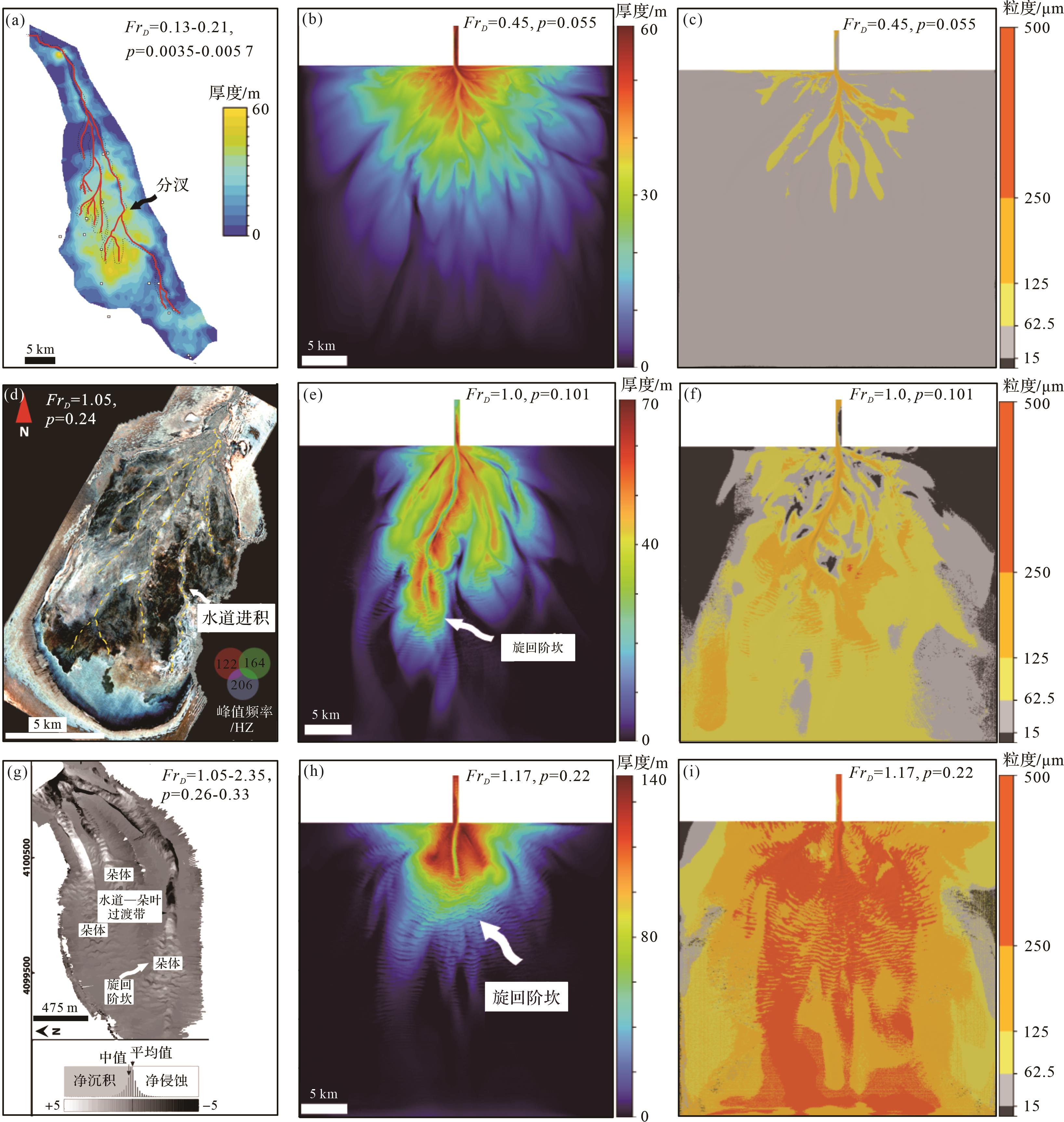
海底扇的形态很大程度上取决于在其表面移动的水道动力学。Wahab et al.^[69]通过数值模拟归纳了密度弗劳德数（Fr_D）和劳斯数（p）控制下的海底扇3种发育模式。类似于刚果现代扎伊尔扇体系^[148]（图8a），亚临界海底扇（Fr_D<1，p<0.055）以内部不对称的分支水道为特征，该模式中砂质沉积物主要富集在水道内部，粉砂—泥质沉积物发育在堤岸、朵体和外扇部位（图8b，c）；墨西哥湾第四纪东部断陷盆地IV号海底扇属临界海底扇（Fr_D=1，p<0.101）模式^[69]（图8d），该模式内部以自生的低弯度水道为特征，水道两侧发育明显的堤岸沉积，沉积物以过路作用为主，砂质沉积物发育在水道、朵体和远端堤岸，粉砂及泥质沉积物主要发育在远端扇（图8e，f）；超临界海底扇（Fr_D=1.17，p=0.22）内部发育单一的自生低弯度主水道。流体厚度的增加和湍流动能的损失导致沉积物以旋回坎的形式在河道内部向上游迁移。水道内部的高剪切应力抑制细粒沉积物沉降，海底扇以砂质沉积物为主，整体呈长条状，类似于现代斯瓦米什海底扇（图8g~i）^[149]。

Figure 8.  Model of submarine fan development based on morphological dynamics (modified from reference [69])

（1） 沉积模拟的局限性。沉积物理模拟基于相似性原理，需要满足几何相似、运动相似和动力相似原则。实验模型通常按一定比例进行缩放，但某些参数（颗粒粒度、深海高压等）难以完全模拟现实世界条件。重力流的运动和动力相似一般通过弗劳德数、雷诺数和希尔兹数等无量纲参数来约束。目前实验中仅能保持单一参数（弗劳德数或希尔兹数）与真实值接近，而雷诺数高于紊流界限值即可。此外，重力流的自加速、卷吸等特性需要一定的时间和空间累积才能够体现出来。数值模拟虽能实现与真实模型一致的时空尺度，但由于纳维—斯托克斯公式的复杂性，计算精度和运算时长往往成反比，一个高精度模型计算时长高达上百万核时^[68]。同时，目前的重力流数值模拟对高浓度颗粒运动以及浊流的底床侵蚀作用模拟效果也不尽如人意^[68]。

（2） 多学科交互。目前重力流研究正迈向定量化的重要阶段，除了传统的野外露头、地下资料、海底监测，沉积物理模拟和数值模拟已成为重力流定量研究的重要手段。沉积物理模拟能够有效刻画重力流沉积过程和动力学特征，同时要求研究者兼具地质学和流体动力学知识背景，以便分析流体水动力现象并总结地质规律。尽管当前的重力流数值模拟软件已相对成熟，但仍需用户具备一定的编程能力，以根据地质背景开发新功能。因此，未来重力流沉积模拟需要地质学、水力学和计算机科学等多学科研究者加强合作，地质资料和过程模拟相结合，推动沉积学理论的发展。

（3） 深水油气开发。深水重力流沉积形成了广泛分布的重力流砂岩，并蕴含着丰富的油气资源。传统的沉积地质研究通过露头、岩心和地震等静态资料对重力流形成机制、沉积特征和发育模式等方面有了宏观的理解，但在定量研究重力流沉积过程和流体转化方面尚显不足。流体搬运过程的差异将直接导致沉积充填样式、砂体展布及叠置样式等沉积结构的不同。借助沉积模拟的手段可以加深重力流沉积过程和分布规律的理解，预测有利沉积体的分布规模和空间组合关系，为深水油气勘探提供理论支持。

（4） 海洋地质灾害。海底滑坡是海底沉积物受多种诱发因素发生大范围移动的地质现象^[150]，其发展演化过程包括滑动、滑塌、碎屑流、浊流四个阶段^[151]。随着世界海洋能源开发不断向深海推进，以海底滑坡为代表的海洋地质灾害正对水下基础设施产生重大威胁。目前关于海底滑坡的相关研究主要集中在海底滑坡形成机制、演化过程和对水下设施冲击评估3个方面。借助沉积物理模拟手段，可以控制初始边界条件，开展不同触发机制条件下的海底滑坡模拟实验，制定斜坡失稳评价标准；从海底滑坡发展规律入手，探究不同地形作用下滑坡冲出距离、堆积宽度、堆积厚度等，建立海底滑坡运动演化模型；最后通过数值模拟开展海底滑坡冲击水下管线实验，建立滑坡冲击力预测公式，评估滑坡破坏性。